CSE355/HW2/HW2.md

HW2

Problem 1

• 1. Points:

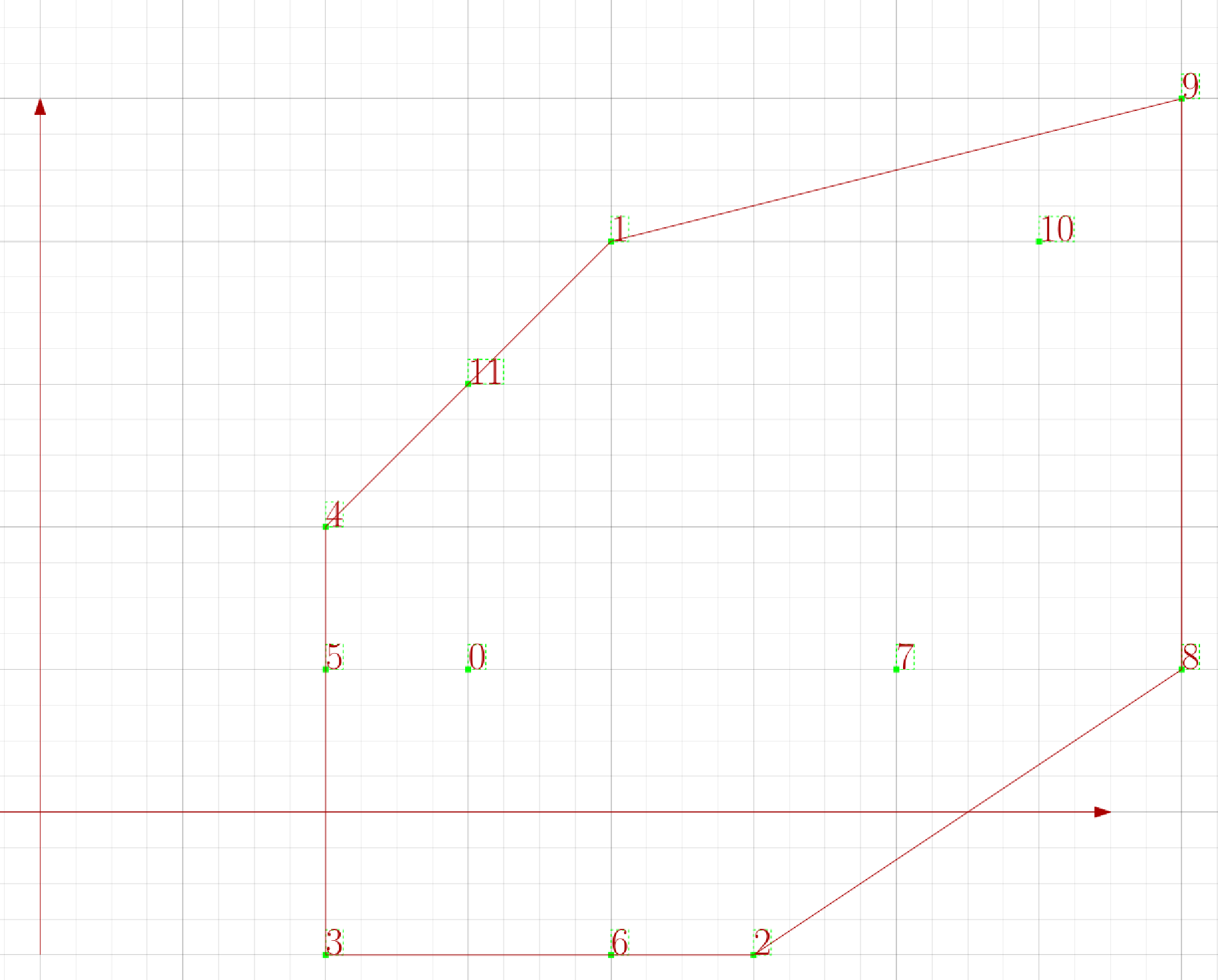
     index	position
     0	(3, 1)
     1	(4, 4)
     2	(5, -1)
     3	(2, -1)
     4	(2, 2)
     5	(2, 1)
     6	(4, -1)
     7	(6, 1)
     8	(8, 1)
     9	(8, 5)
     10	(7, 4)
     11	(3, 3)

     Afer sorting:

     index	position	deleted
     2	(5, -1)	False
     8	(8, 1)	False
     7	(6, 1)	True
     9	(8, 5)	False
     10	(7, 4)	False
     1	(4, 4)	False
     11	(3, 3)	False
     0	(3, 1)	True
     4	(2, 2)	False
     5	(2, 1)	False
     6	(4, -1)	True
     3	(2, -1)	False

     Stack history:

     i	stack
     2	8,2
     3	9,8,2
     4	10,9,8,2
     4	9,8,2
     5	1,9,8,2
     6	11,1,9,8,2
     6	1,9,8,2
     7	4,1,9,8,2
     8	5,4,1,9,8,2
     8	4,1,9,8,2
     9	3,4,1,9,8,2

     image:

• • 1. Because the stack only iterate through points once and exactly once, one point either push in or push in then pop out which take constant time k. So the total time is k*n which is O(n).
  • 2. Consider a square ABDC, p_0 and p_1 is A and B. Then we go to C and push it. Then D, however B-C-D makes a right turn so we pop C then push D. Then we form a convex polygon with points A,B,D, but C is not inside the polygon.

Problem 2

• • QuickHull(p9 , p3 , {p0 , p1, p2 , p4, p5 , p6, p7 , p8, p10 , p 11, p12 })
  • QuickHull(p9 , p5 , {p4 , p11, p8 , p10})
  • QuickHull(p9 , p11 , {p4})
  • QuickHull(p11 , p5 , {p10})
  • QuickHull(p5 , p3 , {p6 , p7, p1})
  • QuickHull(p7 , p3 , {p1})

  recursion stack:

  • QuickHull(p9 , p3 , {p0 , p1, p2 , p4, p5 , p6, p7 , p8, p10 , p 11, p12 })
  • QuickHull((QuickHull(p9 , p5 , {p4 , p11, p8 , p10}), 5, QuickHull(p5 , p3 , {p6 , p7, p1}))
  • QuickHull(QuickHull(p9 , p11 , {p4}), 11, QuickHull(p11 , p5 , {p10}), 5, 7, QuickHull(p7 , p3 , {p1})))
  • QuickHull(QuickHull(p9 , p4 , {}}), 4, QuickHull(p4 , p11 , {}}), 11, QuickHull(p11 , p10 , {}), 10, QuickHull(p10 , p5 , {}), 5, 7, QuickHull(p7 , p1 , {}), 1, QuickHull(p1 , p3 , {})))
  • QuickHull(4, 11, 10, 5, 7, 1)

• • 1. Correct, this is basically the same as Graham scan.
  • 2. Wrong, counter example, c is the smallest angle but c is not a part of convex hull.
  • 3. Wrong, counter example, c is the highest point but if we include c this is not a conven hull.
       
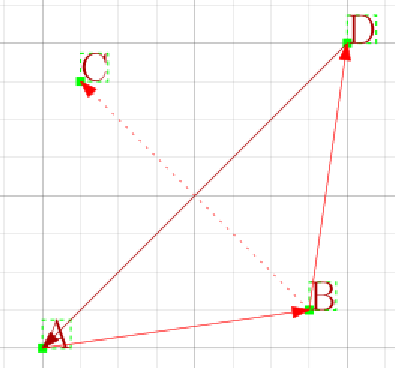
  • 4. Correct, this is a Ellipse with same focuses but different axis. The one with longer axis must contain the one with shorter axis but not vise versa. Thus, the point with highest sum must be a part of convex hull.
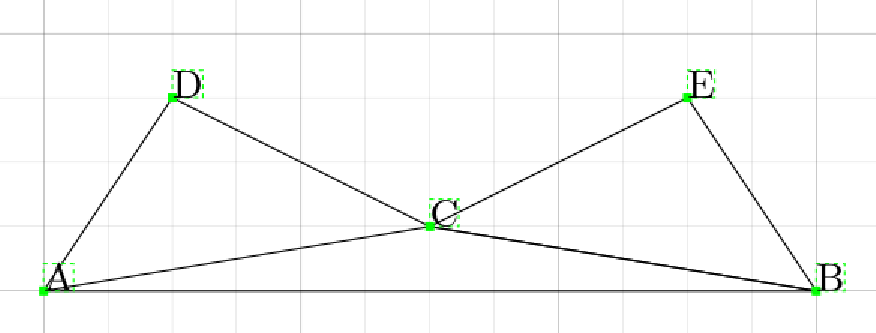
  • 5. Wrong, same graph as question 2, C is the one with minimal distance sum however it is not a part of convex hull.